This week we come to the study of singular integral operators, that is operators of the form
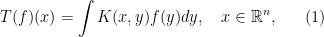
defined initially for `nice’ functions 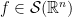 . Here we typically want to include the case where
. Here we typically want to include the case where 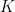 has a singularity close to the diagonal
has a singularity close to the diagonal
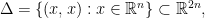
which is not locally integrable. Typical examples are
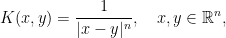

and in one dimension
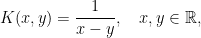
and so on. Observe that these kernels have a non integrable singularity both at infinity as well as on the diagonal 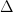 . It is however the local singularity close to the diagonal that is important and will lead us to characterize a kernel as a singular kernel. For example, the kernel
. It is however the local singularity close to the diagonal that is important and will lead us to characterize a kernel as a singular kernel. For example, the kernel
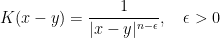
is not a singular kernel since its singularity is locally integrable. Observe that for Schwartz functions 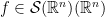 it makes perfect sense to define
it makes perfect sense to define
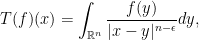
and in fact the previous integral operator was already considered in the Hardy-Littlewood-Sobolev inequality of Exercise 12 in Notes 5 and can be treated via the standard tools we have seen so far.
Thus, if one insists on writing the representation formula (1) throughout 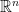 then
then 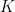 will not be a function in general. Indeed, the discussion in Notes 4 reveals that if the operator
will not be a function in general. Indeed, the discussion in Notes 4 reveals that if the operator  is translation invariant then the kernel
is translation invariant then the kernel 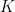 must necessarily be of the form
must necessarily be of the form 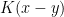 for an appropriate tempered distribution
for an appropriate tempered distribution  :
:
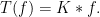
Bearing in mind that there are tempered distributions which do not arise from functions or measures we see that (1) does not make sense in general and it should be understood in a different way. To give a more concrete example, think of the principal value distribution 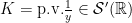 and write
and write

Here we would like to rewrite this in the form
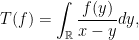
but this does not make sense even for  since the function
since the function 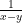 is not locally integrable on the diagonal
is not locally integrable on the diagonal  .
.
In fact, the representation (1) of the operator will not be true in general but we will satisfy ourselves with its validity for functions 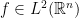 , of compact support, and whenever
, of compact support, and whenever  does not lie in the support of
does not lie in the support of  . Indeed, if
. Indeed, if  has compact support and
has compact support and  then
then 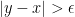 in (1) and thus we are away from the diagonal. Indeed, returning to the principal value example, observe that the integral
in (1) and thus we are away from the diagonal. Indeed, returning to the principal value example, observe that the integral

makes perfect sense when  has compact support and
has compact support and 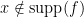 . Continue reading →
. Continue reading →
